Jump to:
Factors Example 1 - Pads Example 2 - Wheel Roller Modulus Of Elasticity Characteristics By Durometer Polyurethane Pad Compression Deflection Percentage Calculator Wheel and Roller Compression Deflection Percentage Calculator Disc or Ring Compression Deflection CalculatorCalculating The Compression/Deflection Of Urethane
Polyurethane, unlike rubber, is a non-compressible elastomer, meaning its volume will not change. In other words if you squeeze it in one place, it will bulge the same amount in another place. For that reason, it makes an excellent material for load-bearing applications.
In load-bearing applications such as isolation pads, bumpers, bushings, rollers and wheels, it is important to know the amount of deflection the part will have when under load. For most applications a range between 5% to 15% deflection is acceptable. However, applications with rapid continuous deflection may need to be limited to lower deflection percentages. We recommend not exceeding 25% deflection regardless of the application.
Factors That Determine The Amount Of Deflection
- Hardness(durometer) of the polyurethane
- Shape of the part
- Amount of load placed on the part
- Condition of the part's loaded surface
Although the formula for calculating compression/deflection was scientifically derived, the many variables involved can make it difficult to precisely predit the outcome. The formula used in example 1 is for pads or cylindrically shaped bumpers only.
Two Important Considerations When Calculating Compression/Deflection
Polyurethanes heat up in dynamic applications which can lower the durometer and in turn, will lower the Young's modulus.
There can be a very large difference in compression/deflection between a part with bonded surfaces, versus the same part between lubricated surfaces. Compression/deflection values for parts compressed between surfaces that are neither bonded nor lubricated, cannot be accurately calculated.
Example 1 - Pads
You have a 92A durometer(hardness) isolation pad that is 6" long by 3" wide and 2" thick, that is under a 3,600 lb load. You want to know how much deflection it will have.
The formula is: L=D x Y x (1+2f2)
D = % of deflection/inch of thickness
L = load or force in psi
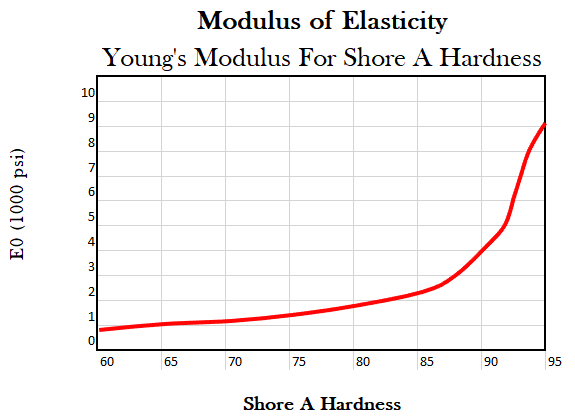
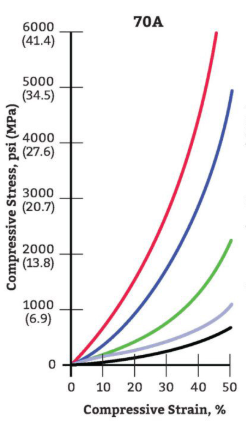
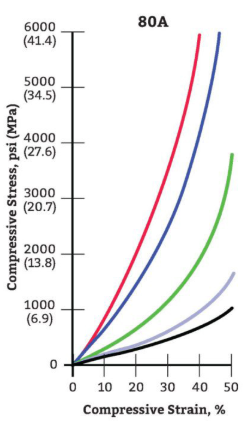
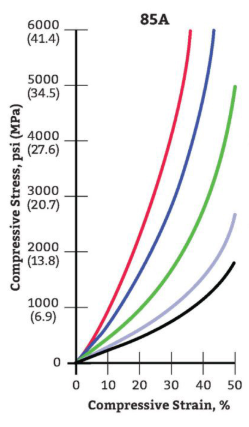
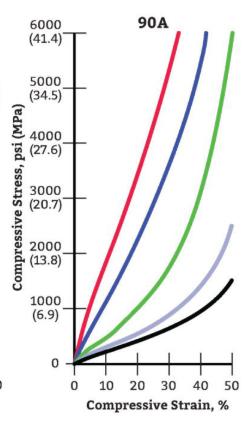
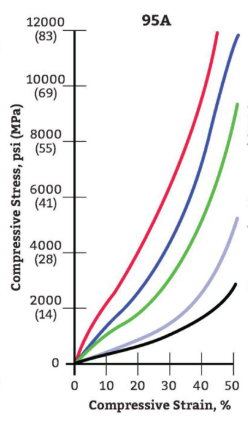
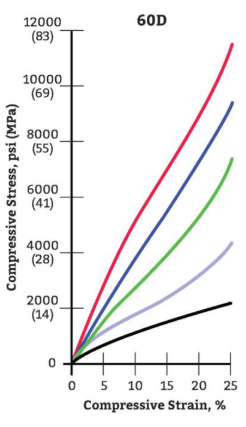
Y = Young's Modulus (see Modulus of Elasticity Diagram below)
f = shape factor
*The shape factor is determined by dividing the area being pressed by the area that is able to bulge.
Solution To Example 1
L = 3600 lbs ÷ 18 square inches (6 x 3) = 200 psi
Y = 4500 psi for 92A durometer(hardness)
f = 18 (6 x 3) area being pressed ÷ by 36 (2x6+2x3+2x6+2x3) area able to bulge = .5
f2 = .52 = .25 therefore (1 + 2f2) = (1 + (2 x .25)) = 1.5
Using the formula above:
200 = D x 4500 x 1.5
200 = 6750D
200 ÷ 6750 = D
D = .0296 per inch of original thickness (2.9%)
2" thick pad x .0296 = .0592" total deflection
Modulus of Elasticity Diagram
As was mentioned above, the condition of the parts loaded surface, has an effect on deflection. When a part is compressed it wants to expand out laterally and that movement changes the shape factor. This is particularly noticeable if the surfaces are lubricated. However, if the surfaces are bonded to a substrate such as metal, the shape factor remains the same. Below is a graph showing the differences in deflection of a bonded part, a dry and clean part and a lubricated part. As you can see, the surface condition of a part can make quite a difference in deflection.
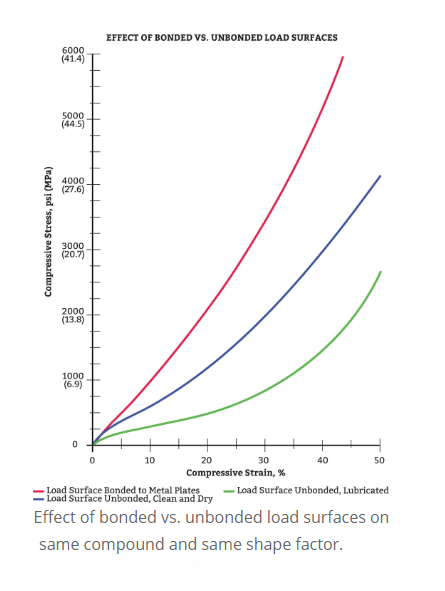
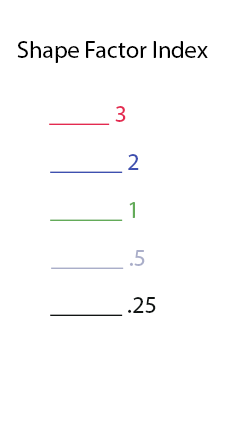
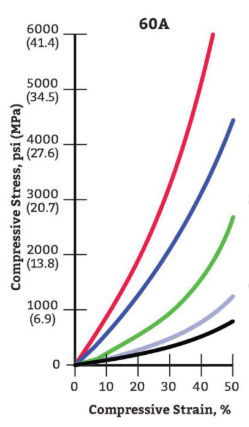
Characteristics By Durometer(Hardness) And Shape Factor
Below are several graphs showing the compression/deflection curve for various shape factors. Each graph is for a different durometer(hardness) of urethane. All samples tested were bonded to metal surfaces.
Example 2 - Wheel/Roller
You have a wheel with a 4" diameter metal core and a 6" diameter polyurethane covering. The wheel is 2" wide and the polyurethane is 92A durometer(hardness). How much will the urethane deflect under a 1000 lb. load?
The formula is:
L = The loading or weight in pounds (not psi)
D = Deflection in inches (not a % deflection)
Y = Young's Modulus (see Modulus of Elasticity diagram above)
W = Width (length of contact surface) of the roller/wheel in inches
a = Inside radius of the polyurethane in inches
b = Outside radius of the polyurethane in inches
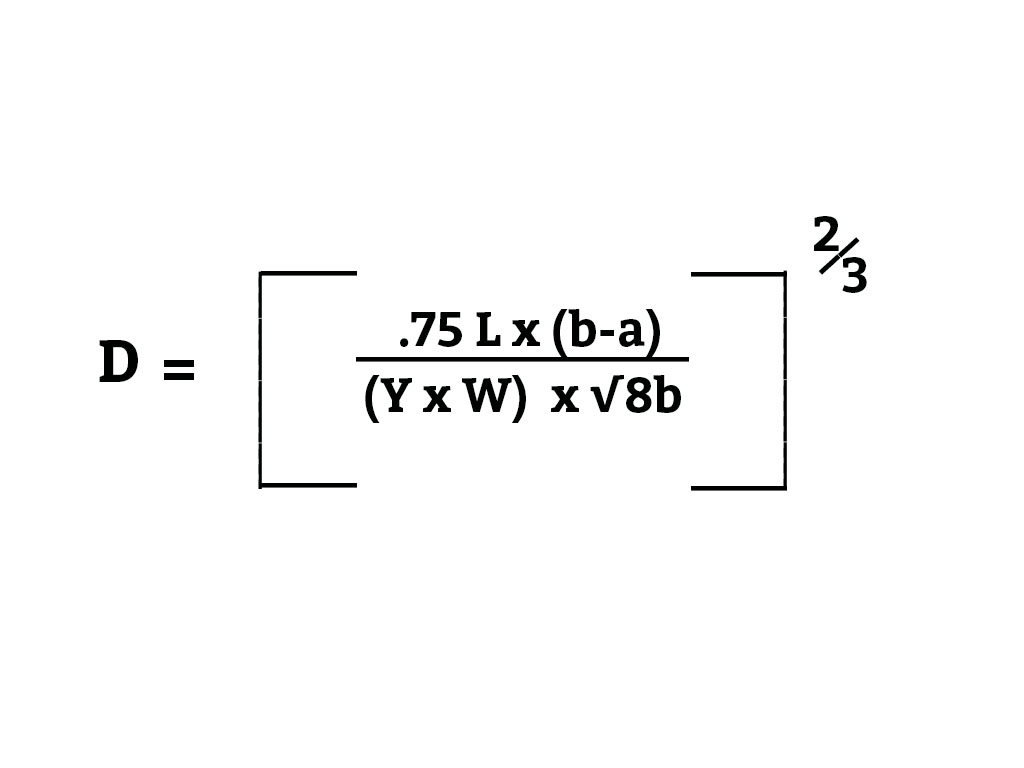
Solution To Example 2
L = 1000 lbs
Y = 4500 for 92A durometer(hardness)
W = 2" wide
a = 2" radius of 4" metal hub
b = 3" radius of 6" urethane covering
Using the formula above:
.75 L = .75 x 1000 = 750
(b - a) = 3 - 2 = 1
Thus .75 L x (b-a) = 750 x 1 = 750
Y x W = 4500 x 2 = 9000
8b = 8 x 3 = 24 √24 = 4.9
Thus Y W x √8b = 9000 x 4.9 = 44,100
| .75 L (b - a) | = |
750 ÷ 44,100 which equals .017 |
|
| Y x W x √8b | |||
.0172/3 = 3√.0172
.0172 = .000289
3√.000289 = .066
Polyurethane Pad Compression Deflection Percentage Calculator
The information given by this calculator is baseline, many factors affect compression such as the surrounding environment, your specific application, and the urethane formulation. Get in touch for assistance in finding the product to suit your individual requirements.
POLYURETHANE PAD COMPRESSION DEFLECTION PERCENTAGE CALCULATOR
Wheel and Roller Compression Deflection Percentage Calculator
The information given by this calculator is baseline, many factors affect compression such as the surrounding environment, your specific application, and the urethane formulation. Get in touch for assistance in finding the product to suit your individual requirements.
Wheel and Roller Compression Deflection Calculator
Disc or Ring Compression Deflection Calculator
The information given by this calculator is baseline, many factors affect compression such as the surrounding environment, your specific application, and the urethane formulation. Get in touch for assistance in finding the product to suit your individual requirements.
Disc or Ring Compression Deflection Calculator
Please note that at least one of the following fields must be filled out to proceed.
Recommended Reads
Stress/Strain: The Causes of Hysteresis
Stress is a measure of the internal reaction force. Strain is the measure of deformation. Hysteresis is the name used to describe the failure of a urethane part…
Ask Our Experts.
Contact us today to learn how we can meet your project’s requirements.